Introduction
If we want to predict the user A's rating of the book X, but we only have the A's rating for some other books and user B's rating of the book X. How can we predict the A's rating of the book X? The easiest way is to simply forecast as average. But we never know with accuracy.
SVD (Singular Value Decomposition) is based on the existing ratings, analysis the favorite degree of the raters for every factors, and get the ranks from analysis result at last. In the above example, there are many factors of the book, such as the cover, author, story, price and etc,.
SVD algorithms make a ranking matrix 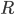 with
with 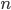 rows and
rows and 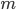 columns as abstract.
columns as abstract. ![R[u][i]](https://xuri.me/wp-content/plugins/latex/cache/tex_41273065fb34a6d9d5f6f00a4bc07648.gif) means that the rank of the object
means that the rank of the object 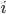 from user
from user 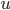 . It can be decomposed into a user factors matrix
. It can be decomposed into a user factors matrix 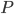 with
with 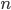 rows and
rows and 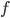 columns (
columns (![P[u][k]](https://xuri.me/wp-content/plugins/latex/cache/tex_d64274704dfdcab6f3159b9f3d3c9936.gif) means that rank of the factor
means that rank of the factor 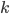 from user
from user 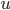 ) and a object factors matrix with
) and a object factors matrix with 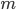 rows and
rows and 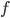 columns (
columns (![Q[i][k]](https://xuri.me/wp-content/plugins/latex/cache/tex_122f2e6ca8445c03e87813f372a149d2.gif) means that rank of the factor
means that rank of the factor 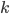 of object
of object 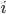 ). This can be represented by the formula like this:
). This can be represented by the formula like this:
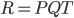
There is an example for decomposed to two matrix. The larger 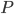 , represents more users prefer the book, larger
, represents more users prefer the book, larger 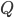 , represents high factor degree. We can predict the user A's rating of the book X after decomposed.
, represents high factor degree. We can predict the user A's rating of the book X after decomposed.
+-------------+------+------+------+
|Rank Matrix R|Book X|Book Y|Book Z|
+-------------+------+------+------+
| User A | 6 | 3 | ? |
+-------------+------+------+------+
| User B | 3 | 2 | 6 |
+-------------+------+------+------+
|
+----------------------+------------------------+
| |
| v
| +-----------------------+--------+----------+
v |Object Factors Matrix Q|Computer|Literature|
+---------------------+--------+----------+ +-----------------------+--------+----------+
|User Factors Matrix P|Computer|Literature| | Book X | 6 | 0 |
+---------------------+--------+----------+ +-----------------------+--------+----------+
| User A | 1 | 0.2 | | Book Y | 3 | 3 |
+---------------------+--------+----------+ +-----------------------+--------+----------+
| User B | 0.3 | 1 | | Book Z | 0 | 6 |
+---------------------+--------+----------+ +-----------------------+--------+----------+
In addition to considering how the user like this book, but also affect by whether they be a strict raters and existing ratings when the user ranking a book in fact. Somebody will give high rank when they got this book has been rank as high value. The factor of how user like this book has been exists, we need to add two new factor to record that another parts to improve the accuracy of the model. After improved formula like this:
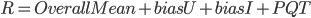
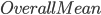 means that average rank of the all books,
means that average rank of the all books, 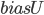 means that the deviation with
means that the deviation with 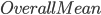 of the user ranking, and
of the user ranking, and 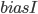 means that the deviation with
means that the deviation with 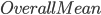 of the book ranks.
of the book ranks. 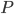 and
and 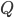 meaning are unchanged and they are all matrices except the
meaning are unchanged and they are all matrices except the  .
.
After decompose, suppose we want to predict user 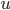 rating for book
rating for book 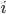 :
:

SVD Implement
Two decomposed matrices get by learning. SVD using stochastic gradient descent learning parameters except the 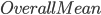 . The learning process can be summarized as this: initial value of each parameter, and then use these parameters to predict, and the predicted results were compared with known rates, adjust each various parameters based on comparison results at last. Adjustment the value of the parameter, making the following formula can take to the minimum:
. The learning process can be summarized as this: initial value of each parameter, and then use these parameters to predict, and the predicted results were compared with known rates, adjust each various parameters based on comparison results at last. Adjustment the value of the parameter, making the following formula can take to the minimum:
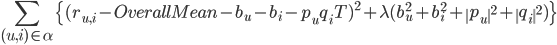
 means that all the training samples, the first part of the parentheses represents the deviation of the current predictions and the actual value, the second part of the parentheses is to prevent overfitting.
means that all the training samples, the first part of the parentheses represents the deviation of the current predictions and the actual value, the second part of the parentheses is to prevent overfitting.
That's the main ideas of SVD.
Reference
Jim Lambers - [The SVD Algorithm]
Chih-Chao Ma - [A Guide to Singular Value Decomposition for
Collaborative Filtering] Department of Computer Science, National Taiwan University, Taipei, Taiwan
Netflix Update: Try This at Home
Matrix Factorization Techniques for Recommender Systems